Kurva fungsi kuadrat y = f( x ) = ax2 + bx + c, a tidak sama dengan nol ( 0 ) berbentuk parabola.
Jika nilai a (+) maka parabola terbuka ke atas dan mempunyai nilai ekstrem minimum
Jika nilai a ( - ) maka parabola terbuka ke bawah dan mempunyai nilai ekstrem maksimum
Koordinat titik puncak / titik ekstrem / titik stationer / titik balik parabola adalah ( Xp , Yp )
dengan :

Xp = absis ( x ) titik puncak = sumbu simetri = absis ( x ) saat mencapai nilai maksimum/minimum
Yp = ordinat ( y ) titik puncak = nilai ekstrem/nilai stationer/nilai maksimum/nilai minimum
B. Sketsa Grafik Fungsi Kuadrat / Parabola
Langkah-langkah dalam membuat sketsa grafik fungsi kuadrat/parabola ( y = ax2 + bx + c ) :
1. menentukan titik potong grafik dengan sumbu x → y = 0
kemudian difaktorkan sehingga diperoleh akar-akarnya yaitu x1 dan x2 . jika kesusahan dalam memfaktorkan coba di cek dulu nilai D nya....
jika D < 0 maka fungsi tersebut memang tidak mempunyai akar-akar persamaan fungsi kuadrat sehingga sketsa grafik fungsi kuadrat tidak memotong sumbu x
jika D > 0 maka fungsi tersebut mempunyai akar-akar persamaan fungsi kuadrat namun kita kesulitan dalam menentukannya... bisa jadi karena angkanya yang susah difaktorkan atau faktornya dalam bentuk desimal. Akar-akarnya dapat kita cari dengan rumus abc :
 setelah kita mendapatkan nilai x1 dan x2 maka titik potong grafik fungsi kuadrat dengan sumbu x :
setelah kita mendapatkan nilai x1 dan x2 maka titik potong grafik fungsi kuadrat dengan sumbu x :( x1 , 0 ) dan ( x2 , 0 )
2. menentukan titik potong grafik dengan sumbu y → x = 0karena x = 0 maka y = c dan titik potong dengan sumbu y = ( 0 , c )
3. menentukan sumbu simetri ( xp ) dan titik ekstrem ( yp )
dari penentuan sumbu simetri ( xp ) dan nilai eksterm ( yp ) diperoleh titik puncak grafik fungsi kuadrat/parabola : ( Xp , Yp )
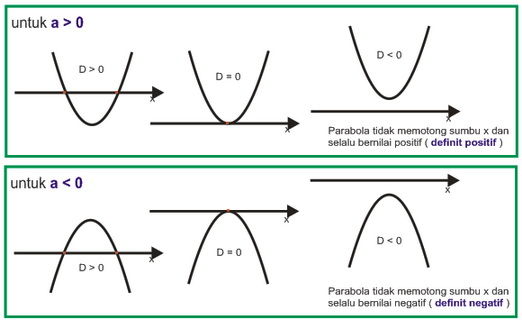
Posisi grafik fungsi kuadrat/parabola terhadap sumbu x
mengulang pembahasan mengenai titik potong sumbu x → y = 0 ada 3 kemungkinan :
D > 0 → grafik fungsi kuadrat memotong sumbu x di dua titik
D = 0 → grafik fungsi kuadrat menyinggung sumbu x di satu titik
D < 0 → grafik fungsi kuadrat tidak memotong sumbu x
dengan menggabungkan dengan nilai a nya dapat dibuat sketsa grafik fungsi kuadrat/parabola :
C. Persamaan Fungsi Kuadrat / Parabola
1. Diketahui tiga titik sembarang
Rumus : y = ax2 + bx + c
nilai a, b dan c ditentukan dengan eliminasi.
2. Parabola memotong sumbu x di dua titik ( x1 , 0 )dan ( x2 , 0 ) dan melalui satu titik sembarang.
Rumus : y = a ( x - x1 ).( x - x2 )
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
3. Parabola menyinggung sumbu x di satu titik ( x1 , 0 ) dan melalui satu titik sembarang.
Rumus : y = a ( x - x1 )2
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
4. Parabola melalui titik puncak ( xp , yp ) dan melalui satu titik sembarang.
Rumus : y = a ( x - xp )2 + yp
nilai a ditentukan dengan memasukkan titik sembarang tersebut ke x dan y.
D. Hubungan Kurva Persamaan Kuadrat / Parabola dan Persamaan Garis Lurus









maksih
BalasHapusMasih blom ngerti bisa diksih contohnya gk pls
BalasHapusMasih blom ngerti bisa diksih contohnya gk pls
BalasHapusmantap
BalasHapusmasih gak ngerti, aku punya bnyak tugas tntang itu, bisa bntu gak?
BalasHapustrimakasih, sangant membantu,...
BalasHapusMau tanya nilai maksimum/minimum itu maksudnya apa ya? Terima kasih :))
BalasHapusMaksimum itu yg tertinggi atau terendah di kurva nya itu. Kalo maksimu itu tertinggi, kalo minimum itu terendah.
Hapusmasih belum ngerti
BalasHapuscara menentuka Determinan itu bagaimana?apakah =0 atau >0 itu bagaimana
Hapusmasih belum ngerti
BalasHapusthank you
BalasHapuspenjelasan anda tidak complete kita gk ngrti
BalasHapuskita gk mudeng dgn penjelasannya..
BalasHapusUdah mudeng sih hehe
BalasHapustolong dong kalo yang ini gimana penyelesaian nya y=-x+1 dari parabola y=x2+2x+1
BalasHapusThank's... sangat membantu :-)
BalasHapusPak jika D<0 itu rumus untuk cari titik potong sumbu x gimana
BalasHapusBingung besok UAS FVCK
BalasHapusnice present
BalasHapusnice present
BalasHapusKalo b nya 0 bagaimana misal y=x^2-9
BalasHapusKalo b nya 0 bagaimana misal y=x^2-9
BalasHapusmakasih banyak saangat bergun untuk penelitian saya
BalasHapusini sumber nya dari buku apa ya?
BalasHapusRibet
BalasHapusRibet
BalasHapusGood job. Its a simple formula😊.
BalasHapusThanks
Makasih.. Sangat membantu
BalasHapusMin bantuin dong jelaskan bentuk kurva dari persamaan kuadrat
BalasHapusX2+y2-2x-25=0
Bang mau nanya nih nyari nilai titik poting gmn ya soalnya masih belom mengerti??klo bisa aama contoh soal
BalasHapusMakasih
Bang mau nanya nih nyari nilai titik poting gmn ya soalnya masih belom mengerti??klo bisa aama contoh soal
BalasHapusMakasih
Mksh gan
BalasHapusTerimakasih sangat membantu..
BalasHapusInsyaallah membantu
BalasHapusgak ngerti
BalasHapusKak kok gak ada contoh soalnya?
BalasHapusMin kalau misalnya di soal dikatakan bahwa kurva memotong smb.x negatif bgmna hubungannya dgn nilai D
BalasHapusApakah D<0 D>0 dan tolong dijelaskan.
Mksih
Makasih kak, membantu banget. Sekarang aku jadi lebih paham.
BalasHapusSangat membantu rumus
BalasHapusMakasih _-
BalasHapusTolong dong kasih contoh
BalasHapusThanks atas ringkasannya sangat membantu
BalasHapusthanks gan sudah share
BalasHapusElemen solder uap
gampang juga ternyata
BalasHapusMamam
BalasHapusCara nyari D nya gimana bro hihi😅😅😅
BalasHapusD=b²–4ac
HapusTerima kasih ringkasannya, sangat membantu
BalasHapusTerima kasih, Sangat bermanfaat
BalasHapus