Bentuk pengintegralan dengan metode subtitusi merupakan versi pengintegralan/kebalikan dari aturan rantai pada differnsial/turunan.
Masih ingatkah turunan berantai!! Perhatikan contoh di bawah ini :
y = ( x2 + 3x + 5 )9 maka turunanya !
Jawab :
y' = 9 ( x2 + 3x + 5 )8 ( 2x + 3)
keterangan :
pangkatnya diturukan sehingga dikali 9 dan pangkatnya berubah dari pangkat 9 menjadi 8, ingat yang bagian dalam kurung tetap... kemudian dikalikan dengan turunan yang di dalam kurung... turunan x2 + 3x + 5 adalah 2x + 3.
Hal ini berarti :
Lalu..Caranya...??
Misal : u = x2 + 3x + 5 maka :

du/dx dibaca turunan fungsi u yang diturunkan variabel x nya....
maka :
contoh soal dan pembahasan integral subtitusi :
1.
Jawab :
* kita misalkan  dan fungsi u dapat diturunkan menjadi
dan fungsi u dapat diturunkan menjadi
* Baru kita subtitusikan ke soal :
Jangan sampai lupa untuk mengembalikan permisalan kita  ya…..
ya…..
2. 
Jawab :
* kita misalkan  dan fungsi u dapat diturunkan menjadi :
dan fungsi u dapat diturunkan menjadi :
* Baru kita subtitusikan ke soal :
3. 
Jawab :
* kita misalkan  dan fungsi u dapat diturunkan menjadi
dan fungsi u dapat diturunkan menjadi
* Baru kita subtitusikan ke soal :
4.  = …
= …
Jawab :
* kita misalkan  maka :
maka :
*sehingga :
5.  …
…
Jawab :
* kita misalkan  maka :
maka :
*sehingga :
dari dua soal terakhir di atas ada cara praktisnya :
Contoh soal lain :
1.

misal :
u = x - 1 maka x = u + 1
du/dx = 7 maka dx = du/7
sehingga :
2.

misal :
u = 4 - x maka x = 4 - u
du/dx = -1 maka dx = du/(-1) = - du
sehingga


banyak kan... contohnya...
Selamat Belajar

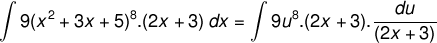
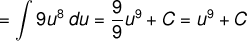











maaf, sekedar saran dan pendapat
BalasHapusmenurut saya, intergral U pangkat 9 itu hasilnya 1/10 U pangkat 10
bukan 9U pangkat 8
kalau 9U pangkat 8 itu turunan
Untuk soal lain no 1 . Knpaaa bsaa du/dx = 7. Tlong jelaskan
BalasHapusSalah ketik tuh
Hapusbukan 7, itu mksdnya 1 mungkin
Hapusthanks admin..
BalasHapusMantap jiwaaaa
BalasHapus1.Integral (7-3x)^4 dx metode substitusi.
BalasHapus2. Integral 9x^2√x^3+5 dx metode substitusi.
Tolonglah bagaimana caranya??
Intergral 3 cos(3- 1 per 2 x) dx tolong caray
BalasHapusKalo soalnya integral (x^2/2+3)^2.x^2 dx
BalasHapuscara menyelesaikannya bagaimana yah ? Mohon jawabannya.terima kasih
Kalo soalnya integral (x^2/2+3)^2.x^2 dx
BalasHapuscara menyelesaikannya bagaimana yah ? Mohon jawabannya.terima kasih
Kansahamnidaaa:) semoga membantu utk UH besik
BalasHapusKalo f'(x) =3x^2+4x-10,jika (-2)=5 maka f(x)? Gimana ya kaaa
BalasHapusmakasih gan, sangat membantu
BalasHapusMakasih
BalasHapusMakasih
BalasHapusTRIMAKASIH SGT MEMBANTU....besok lg yaa...
BalasHapusSmgt
BalasHapusMakasihhh
BalasHapusMembantu banget kak contoh2 soalnya
BalasHapusBelum paham
BalasHapusnice info banget makasih
BalasHapuskartu aku alfamart
Terimakasih mudah dipahami Alhamdulillah👍
BalasHapusTerima kasih, kak.
BalasHapusKurang banyak
BalasHapusMakasih kk
BalasHapusMakasih
BalasHapusMohon di bantu, tentukan integral substitusi intergral (cot²xcscx) dx, bagaimana ya ka??
BalasHapusBagus sekali, barangkali ingin membaca pembahasan soal-soal integral lainnya: https://www.belajarmat.com/pembahasan-soal/pembahasan-soal-integral-dan-cara/
BalasHapus