Metode ini berdasarkan penyelesaian sistem persamaan linear dua variabel dengan metode MATRIKS yang ditampilkan dalam bentuk yang aplikatif untuk menyelesaikan soal secara cepat.
Sebagai contoh diketahui persamaan linear :
x + 2 y = 8 dan x - y = 2
1. Mencari pembilang x
Tutuplah dengan jari tangan atau penggantinya pada bagian x (yang dilingkari). Terus kalikanlah pasangan angka yang ditunjukkan tanda panah, mula-mula atas-bawah lalu bawah-atas. Kemudian selisihkan pasangan atas-bawah dengan bawah-atas.
pembilang x = ( 8 . (-1) ) - ( 2 . 2 ) = -8 - 2 = -12
2. Mencari pembilang y
Tutuplah dengan jari tangan atau penggantinya pada bagian y (yang dilingkari). Terus kalikanlah pasangan angka yang ditunjukkan tanda panah, mula-mula atas-bawah lalu bawah-atas. Kemudian selisihkan pasangan atas-bawah dengan bawah-atas.
pembilang y = ( 1 . 2 ) - ( 1 . 8 ) = 2 - 8 = -6
3. Mencari penyebut untuk x dan y
Tutuplah dengan tangan atau penggantinya pada bagian konstanta (hasil). Terus kalikanlah pasangan angka yang ditunjukkan tanda panah, mula-mula atas-bawah lalu bawah-atas. Kemudian selisihkan pasangan atas-bawah dengan bawah-atas.
penyebut keduanya sama yaitu = ( 1 . (-1) ) - ( 1 . 2 ) = -1 - 2 = -3
4. Hasil akhir (pembilang per penyebut)
x = -12 / (-3) = 4
y = -6 / (-3) = 2
Sepintas metode ini nampak panjang, namun sebenarnya yang kalian tampilkan dalam kertas hitungan hanya pada langkah ke 4 saja. angka-angka yang diperoleh dalam langkah ke 4 adalah angka hasil perkalian dan hasilnya diselisihkan dalam langkah 1 sampai 3 yang kalian kerjakan secara "awangan" (dalam pikiran).He...he...
trus, Metode ini mempunyai beberapa keunggulan :
- mengalikan dan menyelisihkan hasilnya secara "awangan" membuat kalian semakin lancar dalam soal hitungan
- perkalian yang melibatkan garis-garis panah membuat otak kanan kita ikut aktif dalam perhitungan sehingga kita menjadi lebih kreatif.
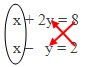


Tidak ada komentar:
Posting Komentar